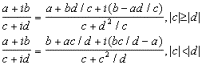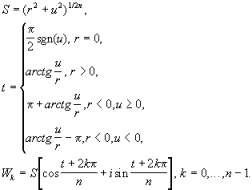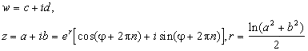Комплексные числа.

План.

1.Понятие комплексного числа

2. Целые комплексные числа

3. Произведение двух комплексных

4. Деление комплексных чисел

5. Корни n-ой степени комплексного числа

6. Действительная степень комплексного числа

7. Комплексная степент комплексного числа.

Комплексные числа, числа вида х + iy, где х и у - действительные числа, а i - так называемая мнимая единица (число, квадрат которого равен -1); х называют действительной частью, а у - мнимой частью К. ч. z = х +iy (обозначают х =Rez, у=Imz). Действительные числа - частный случай коплексных чисел (при у = 0); К. ч., не являющиеся действительными (у ¹ 0), называют мнимыми числами; при х = 0 комплексных чисел. Называют чисто мнимым. Копмлексные числа  z = х+iy и z = х-iy называют комплексно-сопряжёнными. Арифметические действия над комплексными числами производятся по обычным правилам действий над многочленами с учётом условия i²=-1. Геометрически каждое К. ч. х + iy изображается точкой плоскости, имеющей прямоугольные координаты х и у. Если полярные координаты этой точки обозначить через r и j:, то соответствующее копмлексное число. можно представить в виде:

r (cos j + i sin j)

(тригонометрическая, или полярная, форма комплексного числа);

называют модулем копмлексного числа х+iy, а j = arg z - аргументом его. Тригонометрическая форма копмплексного числа особенно удобна для действий возведения в степень и извлечения корня:

[r (cos j + i sin j)] ⁿ = rⁿ (cos nj + i sin nj),

, в частности

, k = 0, 1, …, n-1

По своим алгебраическим свойствам совокупность комплексных чисел образует поле. Это поле алгебраически замкнуто, т. е. любое уравнение xⁿ + a₁x^n-1+...+a_n =0; где a₁,..., a_n –комплексных чисел, имеет (при учёте кратности) среди коплексных чисел точно n корней.

Уже в древности математики сталкивались в процессе решения некоторых задач с извлечением квадратного корня из отрицательных чисел; в этом случае задача считалась неразрешимой. Когда же в 1-й половине 16 в. были найдены формулы для решения кубических уравнений, оказалось, что в так называемом неприводимом случае действительные корни уравнений с действительными коэффициентами получаются в результате действий над комплексными числами. Это содействовало признанию коплексных чисел. Первое обоснование простейших действий с копмплексными числами встречается у Р. Бомбелли в 1572. Однако долгое время к комплексным числам относились, как к чему-то сверхъестественному. Так, Г. Лейбниц в 1702 писал: "Мнимые числа - это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием". В 1748 Л.Эйлер нашёл замечательную формулу e^ij = cosj + isinj, явившуюся первым важным результатом теории функций комплексного переменного, но истинный характер комплексных чисел выяснился лишь к концу 18 в., когда была открыта их геометрическая интерпретация (см. выше). Термин "Копмплексные числа" предложен К. Гауссом в 1831. Введение комплексных чисел делает многие математические рассмотрения более единообразными и ясными и является важным этапом в развитии понятия о числе. Комплексные числа употребляются теперь при математическом описании многих вопросов физики и техники (в гидродинамике, аэромеханике, электротехнике, атомной физике и т.д.). Основные разделы классического математического анализа приобретают полную ясность и законченность только при использовании комрлексных чисел, чем обусловливается центральное место, занимаемое теорией функций комплексного переменного.

Целые комплексные числа, гауссовы числа, числа вида а + bi, где а и b - целые числа (например, 4 - 7i). Геометрически изображаются точками комплексной плоскости, имеющими целочисленные координаты. Целые комплексные числа введены К. Гауссом в 1831 в связи с исследованиями по теории биквадратичных вычетов. Успехи, достигнутые в теории чисел (в исследованиях по теории вычетов высших степеней, теореме Ферма и т.д.) с помощью применения Целых комплексныъ чисел, способствовали выяснению роли комплексных чисел в математике. Дальнейшее развитие теории Целых комплексных чисел привело к созданию теории целых алгебраических чисел. Арифметика целыъ комплексных чисел аналогична арифметике целых чисел. Сумма, разность и произведение целого коплексного числа являются целым комплексным числом (иными словами, целые комплексные числа образуют числовое колъцо).

Произведение двух комплексных чисел вычисляется по формуле:

e+if=(a+ib)(c+id)=(ac-bd)+i(ad+bc)

Деление комплексных чисел. 

Процедура находит частное от деления двух комплексных чисел 

Вычисления проводятся по формулам:

Корни n-ой степени комплексного числа:
Процедура вычисляет все n корней комплексного числа z=r+iu: 

 
Вычисления производятся по формулам 

Действительная степень комплексного числа.

Определяется соотношением.

z^w=(x+iy)^w=r^w(cos(wa)+i sin(wa))

где

a - главное значение аргумента z.

Если w=1/n, то процедура вычисляет главное значение корня n -ой степени из z.

 Комплексная степень комплексного числа.

Пусть заданы комплексные числа

j
 - главное значение аргумента числа z, n- колличество оборотов.

Тогда 

Процедура производит вычисления по данной формуле.